The Other Side of Maths

When we think of maths education, we are often thinking of the methods employed traditionally in schools. The kind of thing that would come to mind is likely to include the processing of abstract symbols, learning mathematical facts and procedures, learning from experts and getting answers among other things

MathsbyColour presents the other side to maths in a number of these areas. We consider these to be an excellent way to supplement a more traditional curriculum based maths programme. These are 4 examples of the other side of maths:

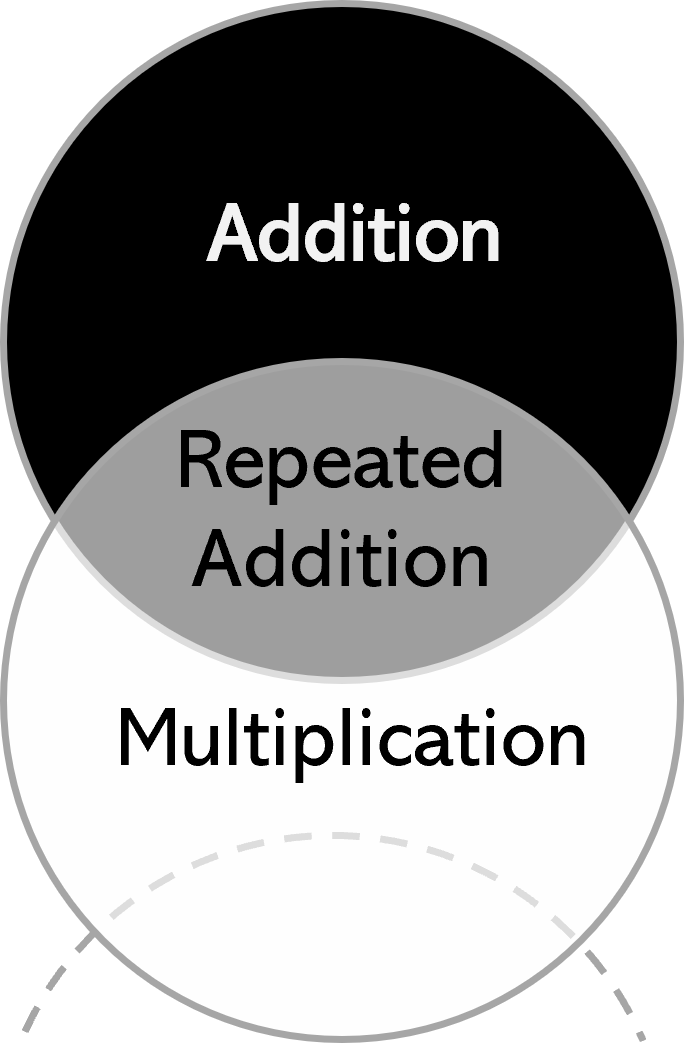
Most early maths builds everything from addition - even multiplication is taught as "repeated addition". MathsbyColour starts with multiplication relationships as fundamental. This reveals the elegant structure underlying all mathematics, making division, fractions, and algebra natural rather than mysterious.

What are Mental Models?

What you think about when you think of numbers and mathematical objects is as important as the methods that you use to do maths in creative maths. Traditional maths teaches facts and procedures like: 7×8=56, memorize the steps for long division. MathsbyColour installs a visual mental model where children see WHY numbers behave as they do. Instead of memorizing that 56 = 7×8, they recognise the colour pattern that reveals 56's mathematical DNA, connecting it instantly to dozens of other relationships.

Visual Tools

Thinking visually is natural for people. Our visual cortex takes up far more mental resource than any other part of the brain. Even when we use abstract symbols, we tend to think of the operations in visual ways. Tools like Numicon and hundred squares help us develop a model of numbers that we are more comfortable with because we can "see" it. We can also see this when balancing algebraic equations and we think of moving expressions around, even though this encourages a problematic mental model of algebra.

MathsbyColour develops all the operations and relationships that you need to master arithmetic using visual means. This allows you to practice with concepts that you might not have the mental capacity to handle abstractly and so develop a consistent idea about arithmetic and the number system that connects the different areas that you will go on to study.

Make an Observation Habit

Instead of drilling facts until they stick, Prime Colours cultivates mathematical curiosity. Children learn to notice patterns, ask questions about what they see, and trust their observations. These thinking habits transform them from passive receivers of mathematical rules into active mathematical thinkers who can tackle unfamiliar problems with confidence.